In this section of our ParaPro Study Guide, We will learn all about decimals. We will cover how to perform various operations with decimals, including addition, subtraction, multiplication, and division. We will also examine the steps to convert fractions to decimals using division. At the end, there will be a five-question quiz to test your understanding.
Decimal Numbers
Decimal numbers contain a whole number and a decimal number with a decimal point separating them.
For example, 28.20 contains 28 as the whole number and 20 as the decimal with a decimal point (.) between them.
Adding and Subtracting Decimal Numbers
To add or subtract two decimal numbers, first align their decimal points. Then, write zeros before the whole part and after the decimal part (if needed to have the same number of digits). Finally, add or subtract the numbers from right to left.
The examples below will take you through these steps.
Example 1
Add 3.9 to 11.26.
First, align the decimal points.
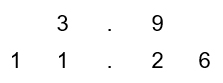
fill in zeros before the whole part and after the decimal part on the top number to match the number place values in the bottom number.
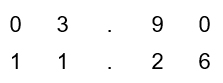
(Note: Writing these additional zeros does not change the value of the number.)
Add normally (as if there was no decimal point).
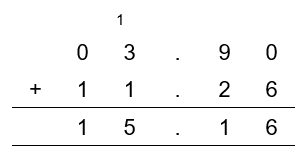
Thus, the sum of 3.9 and 11.26 is 15.16.
Example 2
Subtract 3.99 from 12.02.
Combining the first two steps, we write:

Now, subtract normally (as if there was no decimal point).
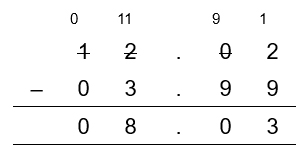
Thus, subtracting 3.99 from 12.02 results in a difference of 8.03.
Multiplying Decimal Numbers
To multiply two decimal numbers, multiply the numbers as though there are no decimal points, and then insert the decimal point as many places from the right as there were to the right of both decimal points in the factors.
When we multiply 10, 100, 1000, etc., to decimal numbers, we shift the decimal point as many times to the right as there are 0’s in 10, 100, 1000, etc.
Let’s apply this to a couple of examples.
Example 3
Multiply 0.34 by 100.
100 has two 0’s.
Thus, when we multiply it with 0.34, we need to shift the decimal point two places to the right.
0.34 × 100 = 34
Example 4
Multiply 1.24 by 6.
Write the numbers without the decimal point.
First we multiply 124 by 6.
124 × 6 = 744
Since 1.24 and 6 have a total of two digits to the right of the decimal, the final answer must also have 2 digits to the right of decimal point.
→ 1.24 × 6 = 7.44
Dividing Decimal Numbers
To divide a decimal number by 10, 100, 1000, etc., we shift the decimal point as many times to the left as there are 0’s in 10, 100, 1000, etc.
To divide a decimal number by another, we multiply both numbers by 10 as many times as there are digits in the decimal places in the number we are dividing by. Then, we follow the rules of long division to work out the result. Let’s go through two examples.
Example 5
Divide 7620 by 1000.
1000 has three 0’s.
Thus, when we divide 7620 by 1000, we need to shift the decimal point three places to the left.
(In a whole number, the decimal point is always to the right of the whole part; in this case, you can think of the number as 7620.0.)
7620 ÷ 1000 = 7.620 or simply 7.62.
Example 6
Divide 0.85 by 0.2.
First, note the number of digits in decimal places in the number by which we need to divide by (0.2.)
Since 0.2 has only one digit in a decimal place, we multiply both 0.85 and 0.2 by 10.
Now we can divide 8.5 by 2 using the long division method as shown below.
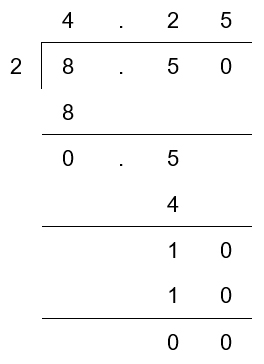
(Note: We stop the division process when we get 0 as our remainder, or otherwise after 2 decimal places unless given further instruction.)
→ 0.85 ÷ 0.2 = 4.25
Converting Fractions to Decimals
To convert fractions to decimals, multiply the fraction in order to have 10, 100, or 1000 in the denominator and then divide the numerator by the denominator. For example, we can multiply $\frac{3}{5}$ by 2 (multiply both the numerator and denominator by 2) to get $\frac{6}{10}$ and then divide 6 by 10 to get 0.6. we can also tell that 0.6 is equal to $\frac{6}{10}$ because it is in the tenths place; the decimal is read as six tenths.
If we cannot perform this conversion, then divide the numerator by the denominator and write the answer to 2 decimal places (or as many as needed).
Let us try an example.
Example 7
Convert the below list of fractions to decimals:
$\dfrac{3}{10}, \dfrac{38}{50}, \dfrac{4}{3}$
For $\dfrac{3}{10}$ :
When we divide $3$ by $10$, we get, $0.3$. So, $\dfrac{3}{10}$ = $0.3$
For $\dfrac{38}{50}$ :
First, multiply both numerator and denominator by $2$ to get $\dfrac{76}{100}$.
When we divide $76$ by $100$, we get $0.76$. So, $\dfrac{3}{10}$ = $0.76$
For $\dfrac{4}{3}$ :
Divide $4$ by $3$ using the long division method to get $1.33$.
$\dfrac{4}{3}$ = $1.33$
Now that you are familiar with the operations of addition, subtraction, multiplication, and division with decimals, take the 5-question quiz below to test your understanding of the content.
